Numerical models
- 3. Introduction A mathematical model is defined as a description from the point of view of mathematics of a fact or phenomenon of the real world, the size of the population to physical phenomena such as speed, acceleration or density.
- 4. Process to develop a mathematical model
- 5. Mental model : first perception of the problem at mental. It is the first play of ideas that intuitively are generated on the issue at hand. Graphic model : the set of images and graphics support that allow you to place the functional relations that prevail in the system to be studied. Verbal Model : it is the first attempt to formalize language characteristics of the problem. In this model performs first formal approach to the problem. Model Types
- 6. Mathematical Model : seeks to formalize in mathematicallanguagerelations and variations you want to represent and analyze. Normally expressed as differential equations and this reason may also be known as differential model. Analytical Model : arises when the differential model can be solved. This is not always possible, especially when the models are posed on differential differential Partial. Physical Model : consists of an assembly that can function as a real testbed. They are usually simplified laboratory scale allow more detailed observations. Not always easy to build.
- 7. Number Model : Arises when using numerical techniques to solve differential models. They are very common when the model has no analytical solution differential. Computational Model : Refers to a computer program that allows analytical or numerical models, can be solved more quickly. They are very useful for implementing numerical models because these are based on iterative process can be long and tedious.
- 8. Model Types Linear Models Polynomials Power Functions Rational functions Trigonometric functions Exponential Functions Logarithm functions Transcendent functions Fig. 1. http://webcache.googleusercontent.com/search?q=cache:trQqOqKXXucJ:www.monografias.com/trabajos12/moma/moma.shtml+CUAL+ES+EL+OBJETIVO+DE+UN+MODELO+MATEMATICO&cd=1&hl=es&ct=clnk&gl=co Example. linear function
- 9. Components of a Mathematical model Dependent variables Independent Variables Parameter Functions of force Operators
- 10. Gradient Fig.2 Elkin slides santafé.2009.Metodos Numerical Engineering function given its gradient vector Gradient Scalar field
- 11. Divergence
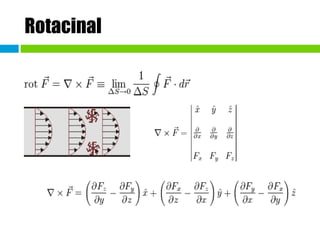
- 12. Rotacinal
- 13. Laplacian Scalar field Vector field
- 14. Finite difference approximation GEOMETRIC DEFINITION Fig.3 Elkin slides santafé.2009.Metodos Numerical Engineering
- 16. Types of differential equations Elliptical Satellite Hyperbolic Laplace equation (Steady state two-dimensional space) Equation heat conduction (Variable time and dimension spatial) Wave equation (Variable time and dimension spatial)
- 17. Fundamental Flow Equation GEOMETRIC FACTOR FLUID DENSITY FLOW RATE POROSITY SOURCES AND / OR SINKS
- 18. Flow in porous media: Darcy's Law c c
- 19. In 1856, in the French city of Dijon, the engineer Henry Darcy was responsible for study of the supply network to the city. It seems that it also had to design filters sand to purify water, so I was interested in the factors influencing the flow of water through the sandy, and presented the results of his work as a appendix to his report of the distribution network. That little appendix has been the basis of all subsequent physico-mathematical studies on groundwater flow. In today's laboratories have equipment similar to that used Darcy, and are called constant head permeameter
- 20. Fig.4 constant head permeameter Q = Caudal Δ h = Potential Difference entre A y B Δ l = Distance between A y B Hydraulic gradient = section Basically a permeameter is a recipient of constant section which makes Flush connecting one end of a high constant level tank. In the other end is regulated by an outflow valve in each experiment also maintains the flow constant. Finally, measure the height of the water column at various points
- 21. Section If the environment changes but the relationship is fulfilled K constant changes. This was called permeability.
- 22. Conservation of Momentum caudal section x velocity Velocidad Darcy : Caudal / Saccion total This is false because the water does not circulate throughout the cross section
- 23. Limitations of Darcy's law The proportionality constant K is not proper or other feature the porous medium. PERMEABILITY INTRINSIC SPECIFIC WEIGHT FLUID VISCOSITY DYNAMICS FLUID
- 24. In some circumstances the relationship between Q and the gradient Hydraulic non-linear. This can happen when the value of K is very low or very high speeds. Darcy is met Darcy is not met can be fulfilled or not
- 25. Equations of State Incompressible fluid Fluid slightly compressible Compressible fluid constant
- 26. Bibliography http://webcache.googleusercontent.com/search?q=cache:trQqOqKXXucJ:www.monografias.com/trabajos12/moma/moma.shtml+CUAL+ES+EL+OBJETIVO+DE+UN+MODELO+MATEMATICO&cd=1&hl=es&ct=clnk&gl=co Elkin slides santafé.2009.Metodos Numerical Engineering F. Javier Sánchez San Román‐‐Dpto. Geología‐‐Univ. Salamanca (España) http://web.usal.es/javisan/hidro